常用的优化方法梯度下降、牛顿法、坐标下降法

    最优化问题在机器学习中有非常重要的地位&＃xff0c;很多机器学习算法最后都归结为求解最优化问题。在各种最优化算法中&＃xff0c;梯度下降法是最简单、最常见的一种&＃xff0c;在深度学习的训练中被广为使用。

    最优化问题是求解函数极值的问题&＃xff0c;包括极大值和极小值。微积分为我们求函数的极值提供了一个统一的思路&＃xff1a;找函数的导数等于0的点&＃xff0c;因为在极值点处&＃xff0c;导数必定为0。这样&＃xff0c;只要函数的可导的&＃xff0c;我们就可以用这个万能的方法解决问题&＃xff0c;幸运的是&＃xff0c;在实际应用中我们遇到的函数基本上都是可导的。

     在机器学习之类的实际应用中&＃xff0c;我们一般将最优化问题统一表述为求解函数的极小值问题&＃xff0c;即&＃xff1a;

其中

       可导函数在某一点处取得极值的必要条件是梯度为0&＃xff0c;梯度为0的点称为函数的驻点&＃xff0c;这是疑似极值点。需要注意的是&＃xff0c;梯度为0只是函数取极值的必要条件而不是充分条件&＃xff0c;即梯度为0的点可能不是极值点。

       至于是极大值还是极小值&＃xff0c;要看二阶导数/Hessian矩阵&＃xff0c;Hessian矩阵我们将在后面的文章中介绍&＃xff0c;这是由函数的二阶偏导数构成的矩阵。这分为下面几种情况&＃xff1a;

如果Hessian矩阵正定&＃xff0c;函数有极小值;如果Hessian矩阵负定&＃xff0c;函数有极大值;如果Hessian矩阵不定&＃xff0c;则需要进一步讨论

       这和一元函数的结果类似&＃xff0c;Hessian矩阵可以看做是一元函数的二阶导数对多元函数的推广。一元函数的极值判别法为&＃xff0c;假设在某点处导数等于0&＃xff0c;则&＃xff1a;

如果二阶导数大于0&＃xff0c;函数有极小值;如果二阶导数小于0&＃xff0c;函数有极大值;如果二阶导数等于0&＃xff0c;情况不定

      直接求函数的导数/梯度&＃xff0c;然后令导数/梯度为0&＃xff0c;解方程&＃xff0c;问题不就解决了吗&＃xff1f;事实上没这么简单&＃xff0c;因为这个方程可能很难解。对于有指数函数&＃xff0c;对数函数&＃xff0c;三角函数的方程&＃xff0c;我们称为超越方程&＃xff0c;求解的难度并不比求极值本身小。精确的求解不太可能&＃xff0c;因此只能求近似解&＃xff0c;这称为数值计算。工程上实现时通常采用的是迭代法&＃xff0c;它从一个初始点
      这张图中的函数有3个局部极值点&＃xff0c;分别是A&＃xff0c;B和C&＃xff0c;但只有A才是全局极小值&＃xff0c;梯度下降法可能迭代到B或者C点处就终止。

      鞍点 :指梯度为0&＃xff0c;Hessian矩阵既不是正定也不是负定&＃xff0c;即不定的点&＃xff0c;鞍点处附近存在有正有负的的二阶导&＃xff0c;即鞍点的hessian矩阵是不定的&＃xff0c;在最优化问题中&＃xff0c;只有hessian矩阵不定时才会出现鞍点&＃xff08;半正定也不会&＃xff09;&＃xff01;。下面是鞍点的一个例子&＃xff0c;假设有函数&＃xff1a;
     在这里&＃xff0c;梯度下降法遇到了鞍点&＃xff0c;认为已经找到了极值点&＃xff0c;从而终止迭代过程&＃xff0c;而这根本不是极值点。对于怎么逃离局部极小值点和鞍点&＃xff0c;有一些解决方案&＃xff0c;在这里我们暂时不细讲&＃xff0c;以后有机会再专门写文章介绍。对于凸优化问题&＃xff0c;不会遇到上面的局部极小值与鞍点问题&＃xff0c;即梯度下降法一定能找到全局最优解。

     梯度下降法有大量的变种&＃xff0c;它们都只利用之前迭代时的梯度信息来构造每次的更新值&＃xff0c;最流行的&＃xff1a;动量优化&＃xff0c;Nesterov 加速梯度&＃xff0c;AdaGrad&＃xff0c;RMSProp&＃xff0c; Adam 优化.详情参见&＃xff1a;快速优化器

黑塞矩阵

     黑塞矩阵&＃xff08;Hessian Matrix&＃xff0c;是一个多元函数的二阶偏导数构成的方阵&＃xff0c;描述了函数的局部曲率。黑塞矩阵常用于牛顿法解决优化问题&＃xff0c;利用黑塞矩阵可判定多元函数的极值问题。在工程实际问题的优化设计中&＃xff0c;所列的目标函数往往很复杂&＃xff0c;为了使问题简化&＃xff0c;常常将目标函数在某点邻域展开成泰勒多项式来逼近原函数&＃xff0c;此时函数在某点泰勒展开式的矩阵形式中会涉及到黑塞矩阵。        

    在数学中, 海森矩阵(Hessian matrix或Hessian)是一个自变量为向量x的实值函数f的二阶偏导数组成的方块矩阵, 此函数如下&＃xff1a; ,如果f的所有二阶导数都存在, 那么f的海森矩阵: 

                                      &＃xff08;1&＃xff09;

 将二元函数的泰勒展开式推广到多元函数&＃xff0c;则在X(0)点处的泰勒展开的矩阵形式为&＃xff1a; 

黑塞矩阵是由目标函数f在点X处的二阶偏导数组成的n∗n阶对称矩阵。

Hessian矩阵性质&＃xff1a;

&＃xff08;1&＃xff09;如果是正定矩阵&＃xff0c;则临界点处是一个局部极小值 
&＃xff08;2&＃xff09;如果是负定矩阵&＃xff0c;则临界点处是一个局部极大值 
&＃xff08;3&＃xff09;如果是不定矩阵&＃xff0c;则临界点处不是极值

判断一个矩阵是否是正定方法 &＃xff1a; 

1、顺序主子式&＃xff1a;实对称矩阵为正定矩阵的充要条件是的各顺序主子式都大于零。 
2、特征值&＃xff1a;矩阵的特征值全大于零&＃xff0c;矩阵为正定&＃xff0c;矩阵的特征值全非负&＃xff0c;矩阵为半正定。矩阵的特征值全小于零&＃xff0c;矩阵为负定。否则是不定的。

from&＃xff1a;https://blog.csdn.net/u010700066/article/details/81836166

二次规划的全局最优&＃xff1a;https://blog.csdn.net/nickkissbaby_/article/details/89419423 

牛顿法

       除了前面说的梯度下降法&＃xff0c;牛顿法也是机器学习中用的比较多的一种优化算法。 但对于非线性优化问题, 牛顿法提供了一种求解的办法. 假设任务是优化一个目标函数 f, 求函数 f的极大极小问题, 可以转化为求解函数 f的导数f′&＃61;0的问题, 这样求可以把优化问题看成方程求解问题(f′&＃61;0).  

    牛顿法的基本思想是利用迭代点处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似&＃xff0c;然后把二次模型的极小点作为新的迭代点(f′&＃61;0的点)&＃xff0c;并不断重复这一过程&＃xff0c;直至求得满足精度的近似极小值。它使用函数f (x)的泰勒级数的前面几项来寻找方程f (x) &＃61; 0的根。牛顿法最大的特点就在于它的收敛速度很快&＃xff0c;而且能高度逼近最优值。

1、基本牛顿法的原理

    考虑同样的一个无约束最优化问题&＃xff1a;

牛顿法的每次迭代就是让一阶导为零&＃xff0c;当且仅当 Δx无线趋近于0。即&＃xff1a;

拟牛顿法&＃xff08;Quasi-Newton Methods&＃xff09;

　　拟牛顿法是求解非线性优化问题最有效的方法之一&＃xff0c;拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷&＃xff0c;它使用正定矩阵来近似Hessian矩阵的逆&＃xff0c;从而简化了运算的复杂度。拟牛顿法和最速下降法一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化&＃xff0c;构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法&＃xff0c;尤其对于困难的问题。另外&＃xff0c;因为拟牛顿法不需要二阶导数的信息&＃xff0c;所以有时比牛顿法更为有效。如今&＃xff0c;优化软件中包含了大量的拟牛顿算法用来解决无约束&＃xff0c;约束&＃xff0c;和大规模的优化问题。

具体步骤&＃xff1a;

    拟牛顿法的基本思想如下。首先构造目标函数在当前迭代
 我们尽可能地利用上一步的信息来选取
从而得到
                                                        

这个公式被称为割线方程。常用的拟牛顿法有DFP算法和BFGS算法。

DFP方法

记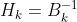&＃xff0c;DFP公式为&＃xff1a;

                   。

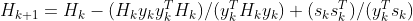 DFP方法是秩-2更新的一种&＃xff0c;由它产生的矩阵B_k是正定的&＃xff0c;而且满足这样的极小性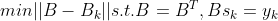&＃xff1a;。

from:http://www.cnblogs.com/shixiangwan/p/7532830.html

坐标下降法

     坐标上升与坐标下降可以看做是一对&＃xff0c;坐标上升是用来求解max最优化问题&＃xff0c;坐标下降用于求min最优化问题&＃xff0c;但是两者的执行步骤类似&＃xff0c;执行原理相同。

例如要求接一个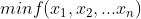的问题&＃xff0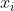c;其中各个是自变量&＃xff0c;如果应用坐标下降法求解&＃xff0c;其执行步骤就是&＃xff1a;

1.首先给定一个初始点&＃x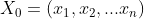ff0c;如

2.for dim&＃61;1:n

固定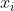;(其中i是除dim以外的其他所有维度)

以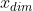为自变量求取使得f取得最小值的&＃xff1b;

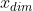  end 

3.循环执行步骤2&＃xff0c;直到f的值不再变化或变化很小。

其关键点就是每次只变换一个维度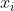,而其他维度都用当前值进行固定&＃xff0c;如此循环迭代&＃xff0c;最后得到最优解。