正题
我们学会了快速傅立叶变换,狄利克雷卷积,现在我们来解决一下快速沃尔什变换。
它主要是解决这样的问题的: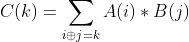 。
。
也就是说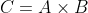
其中那个你看不懂的符号指的是三则运算的其中一种:or,and,xor。
怎么做?
我们来模仿一下解决多项式乘法的过程,我们先是把原数组做一次傅立叶变换,然后再相乘,最后再做一次逆变换。
是否可以把这种方法运用到这里呢?
显然是可以的:我们设一个数组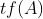 ,它表示A数组FWT变换之后的结果。
,它表示A数组FWT变换之后的结果。
我们要使得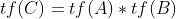 ,其中乘法是按位相乘。
,其中乘法是按位相乘。
然后我们做一次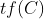 逆变换即可。
逆变换即可。
那么这个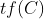 应该怎么找呢?
应该怎么找呢?
三种运算就有三种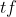
or
我们设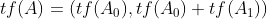
其中+表示按位相加,二元组表示前后相接,也就是说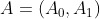 其中0,1表示二进制下标的第一位恰好分为两部分。
其中0,1表示二进制下标的第一位恰好分为两部分。
发现,当我们使得tf这样定义的时候,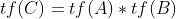 。
。
为什么?
首先来看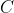 ,
,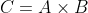 ,明显的当我们把A,B拆开时,贡献到
,明显的当我们把A,B拆开时,贡献到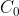 的只有
的只有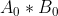 ,而贡献到
,而贡献到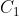 的就是
的就是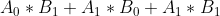 。也就是说
。也就是说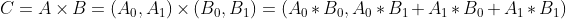 。(因为是或运算啊
。(因为是或运算啊
接着我们就可以知道
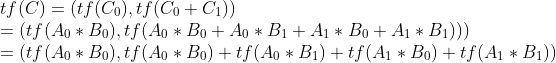
为什么可以拆?因为考虑每个多个数组 加起来和分开 并不影响 每个位置上面的数对后面的影响,具体可以试一下手算。
再看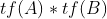 ,这个按位相乘又等于什么呢?相当于前面和前面的相乘,后面的和后面的相乘。
,这个按位相乘又等于什么呢?相当于前面和前面的相乘,后面的和后面的相乘。
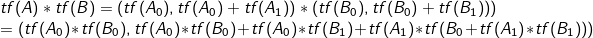
我们知道当只有一个数的时候,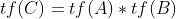 。
。
然后我们就可以知道,只要我们能满足当
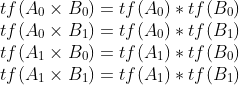
时,那么我们就可以证明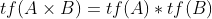 。
。
把上面的四条式子换到上面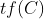 的式子中,可以发现上面所化简的
的式子中,可以发现上面所化简的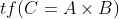 ,
,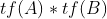 是相等的。
是相等的。
所以我们就证明了当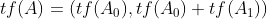 时,
时,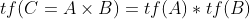 是成立的。
是成立的。
接下来我们就可以用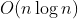 的时间处理出来
的时间处理出来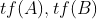 再逐位相乘得到
再逐位相乘得到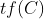 。
。
要求C还不简单吗?
考虑我们怎么从A变为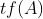 的,是不是先从小的开始,然后将左边的值加到右边。
的,是不是先从小的开始,然后将左边的值加到右边。
我们要变回去,就从最大的区间开始,用用右边的左边的即可。
and
那么与运算其实和或运算差不多。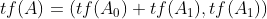 。
。
求逆运算的过程类似。关于证明可以自己推导,十分简单。
xor
抑或运算有点复杂,但是有公式就很好推导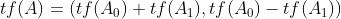 。
。
是不是很鬼畜,然而求逆也是非常简单的,自己推导。
最后,求逆的证明有的博客写得很复杂,其实根本不需要,就相当于将加的减回去即可。
#include
#include
#include
#include
using namespace std;const int maxn=17;
long long a[1<int limit,n;
const long long mod&#61;998244353;long long ksm(long long x,long long t){long long tot&#61;1;while(t){if(t&1) (tot*&#61;x)%&#61;mod;(x*&#61;x)%&#61;mod;t/&#61;2;}return tot;
}void tf_or(long long *now){for(int l&#61;2;l<&#61;limit;l<<&#61;1)for(int i&#61;0;i}void utf_or(long long *now){for(int l&#61;limit;l>&#61;2;l>>&#61;1)for(int i&#61;0;i}void tf_and(long long *now){for(int l&#61;2;l<&#61;limit;l<<&#61;1)for(int i&#61;0;i}void utf_and(long long *now){for(int l&#61;limit;l>&#61;2;l>>&#61;1)for(int i&#61;0;i}void tf_xor(long long *now){long long a,b;for(int l&#61;2;l<&#61;limit;l<<&#61;1)for(int i&#61;0;i}void utf_xor(long long *now){long long a,b;for(int l&#61;limit;l>&#61;2;l>>&#61;1)for(int i&#61;0;i}void FWT_or(){tf_or(a);tf_or(b);for(int i&#61;0;i}void FWT_and(){tf_and(a);tf_and(b);for(int i&#61;0;i}void FWT_xor(){tf_xor(a);tf_xor(b);for(int i&#61;0;i}int main(){inv&#61;ksm(2,mod-2);scanf("%d",&n);limit&#61;1<}