以下是复旦高代教材复习题六的第 19 题或高代白皮书的例 6.18:
习题 1 设 $A,B,C$ 均为 $n$ 阶复方阵, 满足 $C=AB-BA$, $AC=CA$ 和 $BC=CB$, 求证: $C$ 的特征值全为零.
这道题目有多种证法, 其中利用特征值理论进行证明是最直接的方法, 例如大家可以参考复旦高代白皮书例 6.18 的两种证法. 第一种证法是纯代数的方法, 利用了矩阵迹的相关性质以及 Newton 公式, 通过 $C$ 的特征值的幂次计算出了其特征多项式. 这种方法最简单并且可以只要求 $C$ 与 $A,B$ 中的任意一个乘法可交换即可. 第二种证法是纯几何的证法, 利用了如下基本事实: 若两个矩阵乘法可交换, 那么一个矩阵的特征子空间一定是另一个矩阵的不变子空间, 这也是线性变换理论中的重要结论. 当然, 上述习题还有其他的证法, 比如下面的证法三利用了 Jordan 标准型理论来进行证明.
习题 1 的证法三 注意到上述习题的条件和结论在同时相似关系下不改变, 故不妨从一开始就假设 $C$ 是 Jordan 标准型 $J=\mathrm{diag}\{J_1,J_2,\cdots,J_k\}$, 其中 $\lambda_1,\lambda_2,\cdots,\lambda_k$ 是 $C$ 的全体不同特征值, $J_i$ 是对应于特征值 $\lambda_i$ 的根子空间的分块, 即所有属于特征值 $\lambda_i$ 的 Jordan 块拼成的分块对角阵. 由 $AC=CA$, $BC=CB$ 以及高代白皮书的例 6.66 可知, $A=\mathrm{diag}\{A_1,A_2,\cdots,A_k\}$, $B=\mathrm{diag}\{B_1,B_2,\cdots,B_k\}$ 都是分块对角阵且与 $C$ 有着相同的分块方式. 再由 $C=AB-BA$ 可得 $J_i=A_iB_i-B_iA_i\,(1\leq i\leq k)$, 两边同时取迹即得 $\lambda_i=0$, 从而 $k=1$ 且 $C$ 的特征值全为零. $\Box$
上述三种证法都证明了 $C$ 是一个幂零矩阵. 一个自然延伸的问题是, $C$ 的幂零指数 $N=\min\{r\in\mathbb{Z}^+\mid C^r=0\}$ 等于多少? 如果不能给出 $N$ 的确切数值, 那么 $N$ 的最佳上界是多少呢? 由 Cayley-Hamilton 定理可知 $C^n=0$, 从而 $N\leq n$. 下面我们先来证明, $C$ 的幂零指数 $N$ 严格小于 $n$.
引理 2 记号和假设同习题 1, 则 $C$ 的幂零指数严格小于其阶数 $n$.
证明 用反证法来证明结论. 设 $C$ 的幂零指数等于 $n$, 则 $C$ 的特征多项式和极小多项式都等于 $\lambda^n$, 从而 $C$ 的 Jordan 标准型为 $J_n(0)$. 沿用证法三的记号和讨论, 不妨设 $C=J_n(0)$, 则由 $A,B$ 都与 $C$ 乘法可交换以及高代白皮书的例 7.23 可知, 存在多项式 $f(\lambda),g(\lambda)$, 使得 $A=f(C),B=g(C)$, 从而 $C=AB-BA=f(C)g(C)-g(C)f(C)=0$, 矛盾. $\Box$
为了得到 $C$ 的幂零指数的最佳上界, 我们先证明如下引理.
引理 3 记号和假设同习题 1, 设 $f(\lambda)=\sum\limits_{i=0}^ma_i\lambda^i$ 为 $m$ 次多项式.
(i) 对任意的 $k\geq 1$, $AB^k-B^kA=kB^{k-1}C$, 其中约定 $B^0=I_n$;
(ii) $Af(B)-f(B)A=f'(B)C$;
(iii) 若 $B$ 适合 $f(\lambda)$, 即 $f(B)=0$, 则 $C^m=0$.
证明 (i) 对 $k$ 进行归纳, 当 $k=1$ 时, 结论显然成立. 设 $k-1$ 时结论成立, 即有 $AB^{k-1}-B^{k-1}A=(k-1)B^{k-2}C$, 则 $$\begin{align*}AB^k-B^kA&=AB^k-B^{k-1}AB+B^{k-1}AB-B^kA\\ &=(AB^{k-1}-B^{k-1}A)B+B^{k-1}(AB-BA)\\ &=(k-1)B^{k-2}CB+B^{k-1}C=kB^{k-1}C.\end{align*}$$
(ii) 由 (i) 可知, $Af(B)-f(B)A=\sum\limits_{i=0}^ma_i(AB^i-B^iA)=\sum\limits_{i=1}^ma_iiB^{i-1}C=f'(B)C$.
(iii) 由 (ii) 及 $f(B)=0$ 可得 $f'(B)C=0$, 再由 (ii) 可得 $Af'(B)-f'(B)A=f''(B)C$, 从而 $f''(B)C^2=Af'(B)C-f'(B)AC=Af'(B)C-f'(B)CA=0$. 同理不断地做下去, 最后可得 $f^{(m)}(B)C^m=0$, 注意到 $f^{(m)}(B)=m!a_mI_n$, 故 $C^m=0$. $\Box$
习题 1 的证法四 在引理 3 (iii) 中, 取 $f(\lambda)=|\lambda I_n-B|$ 为 $B$ 的特征多项式, 则由 Cayley-Hamilton 定理可知 $f(B)=0$, 故由 (iii) 可知 $C^n=0$, 即 $C$ 是幂零阵. $\Box$
命题 4 记号和假设同习题 1, 设 $m$ 是 $A,B$ 的极小多项式次数的最小值, 则 $C^m=0$. 特别地, $C$ 的幂零指数 $N\leq m$, 并且存在例子使得等号成立.
证明 不妨设 $B$ 的极小多项式 $m(\lambda)$ 的次数为 $m$, 它小于等于 $A$ 的极小多项式的次数. 在引理 3 (iii) 中代入 $m(\lambda)$, 即可得到 $C^m=0$. 我们举例说明这样的 $m$ 可以等于幂零指数. 设 $A=\begin{pmatrix} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$, $B=\begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$, $C=AB-BA=\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{pmatrix}$. 容易验证 $C$ 与 $A,B$ 都乘法可交换, $A,B$ 的极小多项式都是 $\lambda^2$, 并且 $C$ 的幂零指数就等于 2. $\Box$
一般来说, $C$ 的幂零指数是很难确定的. 例如, 若 $A,B$ 乘法可交换, 则 $C=0$, 此时 $C$ 的幂零指数等于 1, 但 $A,B$ 的极小多项式次数的最小值可以等于 $n$. 因此命题 4 说明: $A,B$ 的极小多项式次数的最小值只是幂零指数的最佳上界而已. 接下去我们考虑习题 1 的一个变形, 令 $C=\mu B$, 其中 $\mu$ 是非零复数. 在这种情形下, $C$ 与 $B$ 乘法可交换, 但并不要求 $AC=CA$ 成立, 所以下面的讨论跟上面的讨论并没有太多的关联. 这个变形是一道常见的考研试题, 也是 2009 年第一届全国大学生数学竞赛预赛的一道代数试题 ($\mu=1$ 的情形).
习题 5 设 $A,B$ 均为 $n$ 阶复方阵, 满足 $AB-BA=\mu B$, 其中 $\mu$ 为非零复数. 求证: $B$ 的特征值全为零, 并且 $A,B$ 有公共的特征向量.
证明 注意到习题 1 的证法一只利用了 $BC=CB$ 这一条件, 所以作为证法一的特例, 马上可以得到 $B$ 的特征值全为零. 设 $V_0$ 为 $B$ 属于特征值零的特征子空间, 容易验证 $V_0$ 是 $A$-不变子空间. 考虑 $A$ 在 $V_0$ 上的限制, 这个线性变换一定存在特征向量 $\alpha$, 于是 $\alpha$ 就是 $A,B$ 公共的特征向量. $\Box$
我们同样可以考虑习题 5 自然延伸的问题, 那就是 $B$ 的幂零指数的最佳上界是多少呢? 因为习题 1 和习题 5 在条件上有差别, 所以命题 4 的结论并不适用于习题 5, 故我们转而证明如下结论.
命题 6 记号和假设同习题 5, 设 $A$ 有 $k$ 个不同的特征值, 则 $B^k=0$. 特别地, $B$ 的幂零指数 $N\leq k$.
证明 我们利用 $A$ 的 Jordan 标准型来进行证明. 任一复数 $z&#61;a&#43;bi$ 都等同于复平面上的点 $(a,b)$, 规定实部的权重大于虚部的权重, 故可对全体复数进行实部加虚部的字典排序. 对 $A$ 乘以 $1/\mu$ 不改变命题 6 的条件和结论, 故不妨设 $\mu&#61;1$. 注意到命题 6 的条件和结论在同时相似关系下不改变, 故不妨从一开始就假设 $A$ 是 Jordan 标准型 $J&#61;\mathrm{diag}\{J_1,J_2,\cdots,J_k\}$, 其中 $\lambda_1>\lambda_2>\cdots>\lambda_k$ 是 $A$ 的全体不同特征值, $J_i$ 是对应于特征值 $\lambda_i$ 的根子空间的分块, 即所有属于特征值 $\lambda_i$ 的 Jordan 块拼成的分块对角阵. 设 $B&#61;(B_{ij})_{k\times k}$ 为对应的分块, 则由 $AB-BA&#61;B$ 可得 $J_iB_{ij}&#61;B_{ij}(J_j&#43;I)$. 注意到 $J_i$ 的特征值全为 $\lambda_i$, $J_j&#43;I$ 的特征值全为 $\lambda_j&#43;1$, 若 $i\geq j$, 则 $\lambda_i\leq \lambda_j<\lambda_j&#43;1$, 故 $J_i$ 与 $J_j&#43;I$ 没有公共的特征值, 由高代白皮书的例 6.63 可知 $B_{ij}&#61;0$; 若 $i 例 7 将 $AB-BA&#61;\mu B$ 改写为 $AB&#61;B(A&#43;\mu I_n)$, 取矩阵 $A&#61;\begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix}$. 当 $\mu&#61;1$ 时, 取 $B&#61;\begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}$, 则命题 6 中的 $k&#61;2$ 就等于 $B$ 的幂零指数, 即达到了最佳上界; 而当 $\mu&#61;2$ 时, 满足上述条件的矩阵 $B&#61;0$, 这个结论比命题 6 的结论 $B^2&#61;0$ 来的更强. 因此, 对应于不同的 $\mu$, $A$ 的不同特征值的个数并非都是 $B$ 的幂零指数的最佳上界. 下面我们来做一点改进, 使得上界达到最佳. 命题 8 设 $R(A)$ 是 $A$ 的谱集, 令 $$m&#61;\max\limits_{\lambda\in R(A)}\{s(\lambda)\in\mathbb{Z}^&#43;\mid \lambda&#43;j\mu\in R(A)\,(\forall\,0\leq j 证明 由 Jordan 标准型理论可知, 存在 $\mathbb{C}^n$ 的一组基 $\{e_1,e_2,\cdots,e_n\}$, 使得 $A$ 在这组基下的表示矩阵为 Jordan 标准型 $J&#61;\mathrm{diag}\{J_{r_1}(\lambda_1),J_{r_2}(\lambda_2),\cdots,J_{r_k}(\lambda_k)\}$. 对特征值 $\lambda_1$ 而言, 我们有 $$Ae_1&#61;\lambda_1e_1,Ae_2&#61;e_1&#43;\lambda_1e_2,\cdots,Ae_{r_1}&#61;e_{r_1-1}&#43;\lambda_1e_{r_1}.$$ 设 $s_1&#61;s(\lambda_1)$, 即满足 $\lambda_1&#43;j\mu\in R(A)\,(\forall\,0\leq j 由定义可知, 命题 8 中的 $m$ 小于等于 $A$ 的不同特征值的总个数, 因此命题 8 提供的上界比命题 6 提供的上界更加精确. 例 7 的 $\mu&#61;2$ 的例子中, $m&#61;1$ 就是 $B$ 的幂零指数, 这也说明命题 8 给出的是最佳上界. 注 命题 6 是复旦大学数学学院 16 级高等代数 II 期中考试第五大题的推广, 命题 6 的证明由 16 级陈杰新同学给出, 命题 8 的证明由 16 级朱民哲同学给出.




![[大整数乘法] java代码实现](https://img1.php1.cn/3cd4a/24c6f/9f3/0133bb25da242824.jpeg)
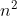

 京公网安备 11010802041100号
京公网安备 11010802041100号